UTILIZATION OF CATEGORICAL METHODS
Advantages of categorical methods
- The parameters are easily interpretable (probabilities or odds of outcome).
Disadvantages of categorical methods
- If continuous variables are categorized, a level of detail is lost.
- Categories may lack clinical relevance, may include too few observations, or result in empty cells when many categories are created
WHAT ARE CATEGORICAL METHODS?
- Regression models incorporate binary or multi-category outcome variables to determine risk or log odds of one category of an outcome compared to the reference category of the same outcome. Predictors can be either categorical or continuous.
- Statistical methods that utilize categorical variables require different approaches, compared to continuous variables, due to the differences in statistical summaries and distributions.[1]
- Categorical variables are best summarized using frequencies and percentages, which can be thought of as probabilities. The frequencies, by definition, must be greater than zero (non-negative numbers).
- The natural logarithm is a commonly used transformation to ensure data is greater than zero (non-negative) and displays as a linear function of the predictor variable(s). However, this assumption can be relaxed by using flexible splines or other nonlinear functions.
- The probabilities by definition must be between 0 and 1, and several transformation “link” functions can be used to map the probabilities from (0, 1) into an unconstrained scale (-∞, +∞). Common transformations include logit and probit.
- Contingency tables, or two-by-two tables (a special case for two variables with two categories each), can provide a useful summary of categorical predictor and outcome variables. For example, Table 1 shows the stunting status at birth with the corresponding maternal Height category of the mother.
Ordinal Logistic Regression[3]
When trying to understand risk factors that are associated with ordered categorical outcomes, ordinal logistic regression (OLR) can be useful as described in the example that follows. In the example, a set of independent variables (predictors) are selected to predict the odds of outcome being one of the ordered response categories (dependent variable).
This model assumes the proportionality of odds for each category of the response variable. In other words, the effect of the predictor is the same across the different categories, which means that for a given change of the predictor, the odds from passing from one category to the next is the same regardless of what category we are starting at. This test for proportionality is discussed further and displayed in the ki example below and can be relaxed if it does not hold.
Example: Ordered categorical model for LAZ
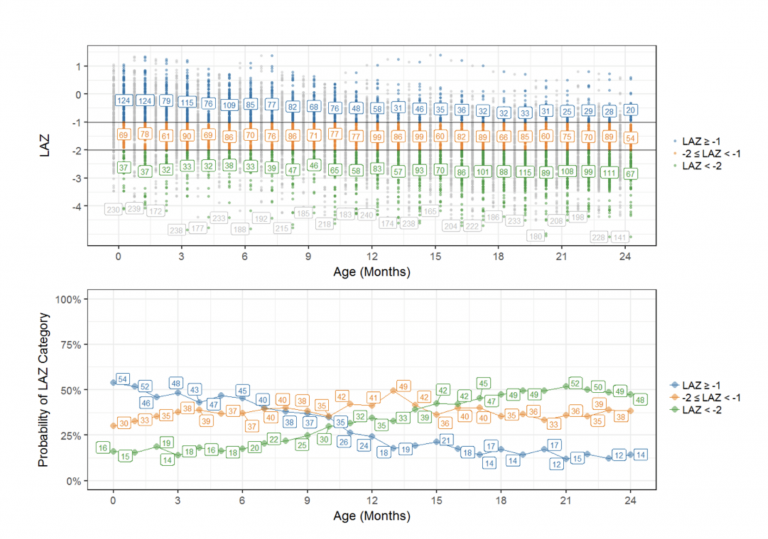
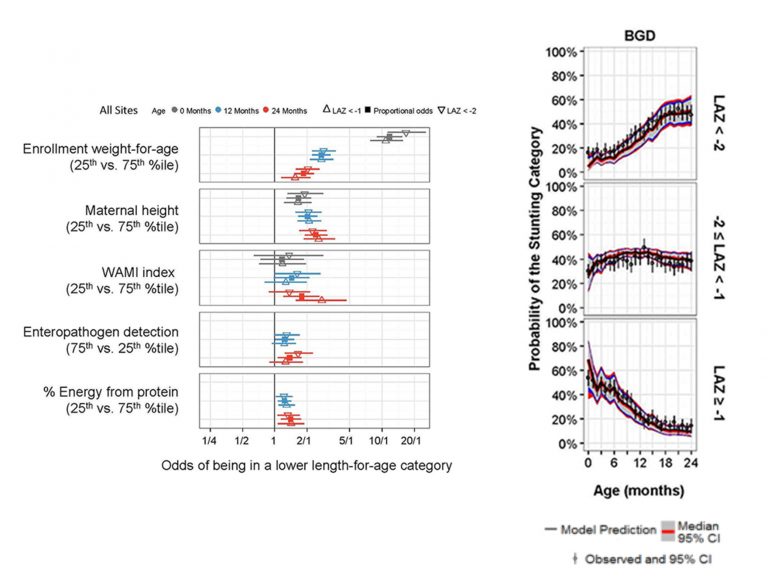
As an example, an previous ki models have defineda categorical outcome variable for length-for-age-zscore (LAZ) where participants were defined as being stunted if LAZ < -2, at-risk for stunting if LAZ was between -2 and -1, and not stunted if LAZ ≥ -1. LAZ was regressed on continuous and categorical variables including age, mother’s height, presence of enteric pathogens in stool, % energy from protein, enrollment LAZ and other important variables.[4] In Figure 1(upper panel), LAZ values have been color-coded to represent the 3 categories: stunted, at-risk for stunting, and not stunted.At age 0 Months, we had 37 infants below -2 (green points) from the total of 230 infants (shown in gray). This translates to the 16% shown age 0 Months in the lower panel of Figure 1. The probability of being stunted (LAZ < -2) is increasing over time (follow the green line).
To relate LAZ as an outcome of potential risk factors, ordinal regression analysis was utilized because of the natural order of the constructed LAZ categories .A linear piecewise spline age with breakpoints every 6-month intervals was necessary to describe the nonlinear relationship between age and the probability of LAZ category.