WHAT IS FUNCTIONAL DATA ANALYSIS?
Information about curves, surfaces, or anything else that varies over a continuum, such as growth over time is called functional data.
Time series data are an example of functional data.[2] Functional data are often characterized by:
- High-frequency measurements
- An underlying “smooth” but complex process
- Repeated observations
- Multi-dimensionality
Functional data analysis (FDA) is a set of statistical tools that enables a more accurate summary and analysis of these types of data.[3]
WHAT IS FUNCTIONAL PRINCIPAL COMPONENT ANALYSIS?
Principal Component Analysis (PCA) is a statistical procedure used to investigate and characterize dominant modes of variation in multivariate data, called principal components, or principal modes of variation.[3] PCA is used across disciplines as a form of dimensionality reduction.[3]
Analogously, Functional Principal Component Analysis (FPCA) is a method for investigating and characterizing the dominant modes of variation in functional data.
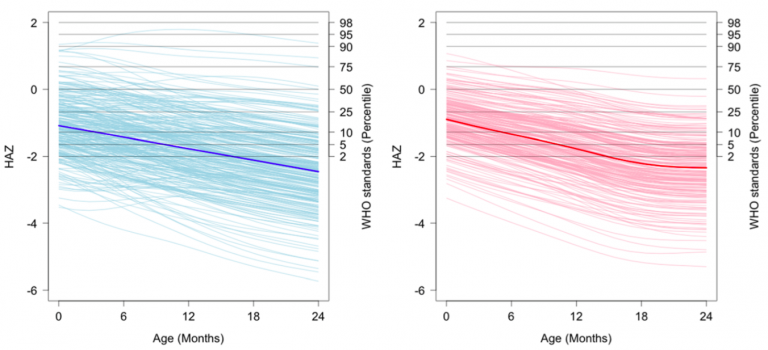
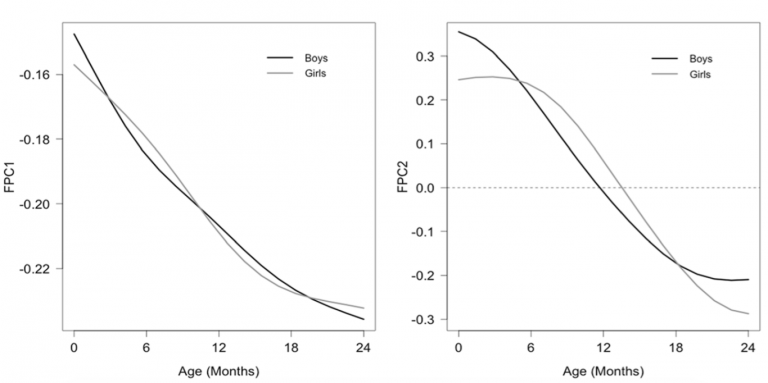
The visualization below (Figure 1) shows an example of FPCA inputs and output.[1]